La sección de El Tiempo ocupa una parte destacada en los telediarios de todas las cadenas. Esta sección, aparte de informarnos de la meteorología de la jornada, nos ha ayudado a comprender conceptos como la probabilidad de lluvia o la imposibilidad de saber un lunes si el domingo podremos ir a la playa.
En el caso de las epidemias, otro fenómeno muy difícil de explicar, la incertidumbre de cuándo llegará (o llegó) el pico y cuánta gente va a ingresar en el hospital la semana que viene invita a usar una variedad de modelos matemáticos llamados cadenas de Márkov.
En nuestro objetivo de acercar a la sociedad los instrumentos matemáticos que nos ayudan a enfrentar la actual pandemia, nos hacemos eco de la figura de un matemático excepcional, Andréi Andréyevich Márkov, el inventor de las cadenas que llevan su nombre.
Estudios e inicios en la probabilidad
Márkov nació en Riazán, Rusia, el 14 de junio de 1856. Su padre, hijo de un diácono rural, estudió en un seminario, consiguiendo posteriormente un empleo en el Departamento Forestal en San Petersburgo. Andréi era el mayor de los dos hijos varones en una familia numerosa. Su hermano menor, Vladimir, muerto prematuramente de tuberculosis, había conseguido en un corto espacio de vida una gran reputación como buen matemático.
El primogénito era un niño con una salud delicada que llevó muletas hasta los diez años pero, ya en la secundaria destacó en Matemáticas, llamando la atención de sus profesores.

Era obvio que Márkov iba a estudiar esta materia y así lo hizo en la prestigiosa facultad de Física y Matemáticas de la Universidad de San Petersburgo. Allí recibió una fuerte influencia del brillante matemático Pafnuty Lvovich Chebyshev (Okátovo 1821 – San Petersburgo 1894).
Márkov se graduó en 1878 y comenzó su trabajo de máster sobre teoría de números (aproximación racional), una tesis que fue muy alabada y considerada uno de los mejores tratados sobre el tema en esa época. Esto le permitió seguir su carrera como profesor de la universidad y conseguir el doctorado en 1884. Dos años después, se convirtió en adjunto de la Academia de Ciencias de San Petersburgo a propuesta de Chebyshev, aunque siguió manteniendo su vinculación con la universidad.
Fue en 1900 cuando Márkov comenzó a interesarse por la teoría de probabilidad, tema en el que obtuvo resultados muy brillantes, incluido el descubrimiento de las cadenas que llevan su nombre.
Chebyshev, Kolmogorov y Márkov son los grandes nombres que usaron elementos de la teoría de la medida para convertir la teoría de probabilidad en una de las áreas más rigurosas y respetadas de las matemáticas.
Márkov no trabajó pensando en las posibles aplicaciones prácticas de las cadenas que descubrió. De hecho, la única área donde las empleó fue en la literatura, contando vocales y consonantes, quizás por su gran amor a la poesía. Sin embargo, como mostraremos a continuación, las aplicaciones de las cadenas de Márkov son de gran utilidad práctica.
Las cadenas de Márkov
De manera intuitiva, una cadena de Márkov en tiempo discreto (por sencillez) es un proceso estocástico que evoluciona en tiempo discreto o etapas y tiene la propiedad markoviana que dice: “el futuro depende de lo que pasa en el presente, pero no del pasado estricto”.
Así, tendremos unos estados E₁, E₂, E₃,… de manera que se pasa de uno a otro por una matriz de transición en una etapa. La cardinalidad (número de elementos) del conjunto de estados es numerable, es decir, es un conjunto finito o con la misma cardinalidad que los números naturales.
La matriz de transición en cada etapa tiene como elementos a las probabilidades de paso de un estado a otro cuando el proceso evoluciona desde una etapa n a la etapa siguiente n+1. Por lo tanto, está compuesta de números reales positivos entre 0 y 1, de manera que la suma de cada fila o columna, según la disposición de los estados inicial (en la etapa n) y final (en la etapa n+1), es 1.
Aplicación en medicina
El siguiente es un ejemplo muy sencillo. En una unidad de cuidados intensivos, los pacientes se clasifican (triage) atendiendo a su estado: crítico, serio y estable. Cada día se actualizan las clasificaciones de acuerdo con la evolución histórica de los pacientes admitidos en la unidad hasta ese momento, de modo que las frecuencias relativas de cambios de estado de un paciente son:
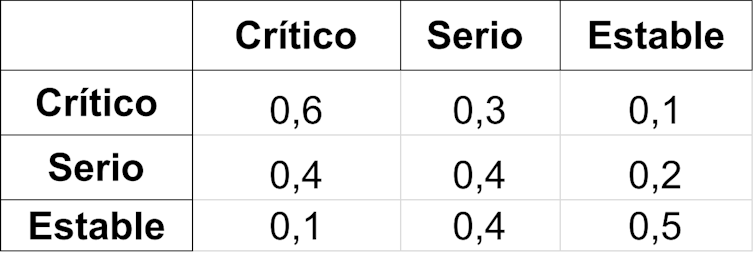
En la disposición anterior, las entradas por filas están asociadas al estado del paciente en el día n y las columnas se refieren a su estado en el día n+1. Entonces, podríamos tomar como matriz de transición en una etapa:
Las filas suman 1. Una representación gráfica como la siguiente nos puede ayudar a entender mejor la dinámica de cambio entre estados de un paciente en dos días consecutivos:
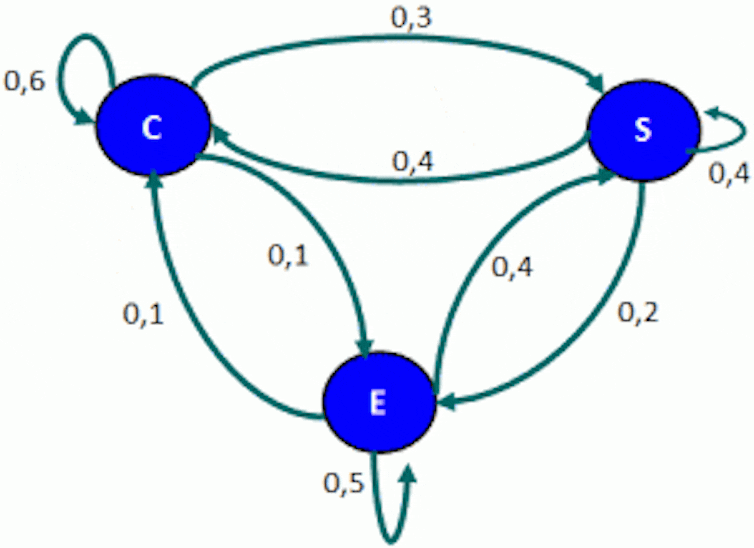
Con un gráfico como este podemos calcular probabilidades en más de una etapa. Por ejemplo, la probabilidad de pasar del estado crítico C a estable E en dos días. Hay tres posibles caminos, dependiendo del estado C, S y E del paciente después del primer día:
C –> C –> E
C –> S –> E
C –> E –> E
Solo tenemos que multiplicar las probabilidades y sumar de la forma:
0,6 × 0,1 + 0,3 × 0,2 + 0,1 × 0,5 = 0,17
Es decir, un paciente ingresado en estado crítico C evolucionará al estado estable E en dos días en un 17 % de las ocasiones. Evidentemente, estas probabilidades pueden cambiar conforme aparecen nuevos tratamientos, o podrían definirse distintos estados de la cadena atendiendo a la edad del paciente, etc. Todas estas generalizaciones enriquecerían la cadena de Márkov, pero la idea general seguiría siendo la misma.
Compromiso político y social
Márkov era una persona comprometida políticamente en una época, principios del siglo XX, de transición agitada de Rusia. Por ejemplo, cuando a Maksim Gorky se le retiró su nombramiento como académico de la Academia de Ciencias por razones políticas, protestó enérgicamente.
En 1913, el matemático se negó a secundar la celebración del tercer centenario del zarismo para celebrar, por su cuenta, el segundo aniversario de la Ley de los Grandes Números.
Cuando triunfó la Revolución Rusa de 1917, Márkov solicitó que le enviaran a un pequeño pueblo del interior, Zaraisk, a enseñar en la escuela local de manera gratuita y así contribuir a la mejora de la pobre sociedad rural.

Aquejado de graves problemas de salud, este brillante matemático ruso falleció en San Petersburgo el 20 de julio de 1922. Murió a los 66 años de edad debido a la infección generalizada producida por una de las varias operaciones quirúrgicas de rodilla a las que fue sometido.
Una versión de este artículo fue publicada originalmente en el blog Matemáticas y sus fronteras, de la Fundación para el Conocimiento madrid+d.
No hay comentarios:
Publicar un comentario
Quin és el teu Super-Comentari?